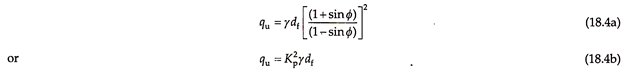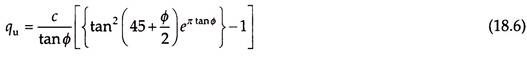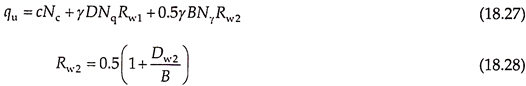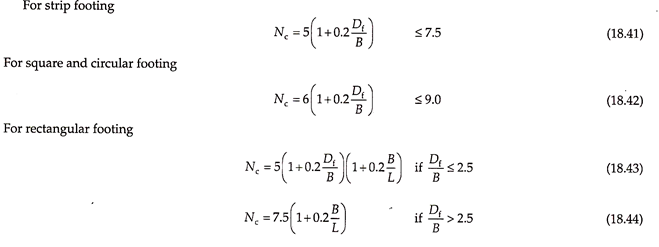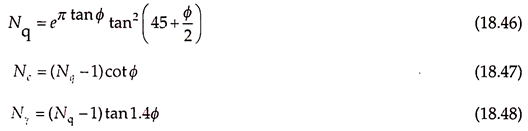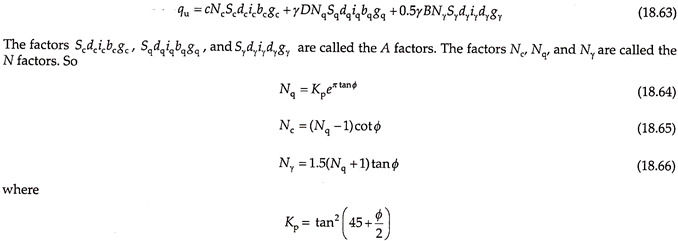Bearing Capacity of the Soil: 7 Theories | Soil Engineering

The following point highlights the seven main theories for determining bearing capacity of the soil. The theories are: 1. Rankine’s Theory of Bearing Capacity 2. Prandtl’s Theory of Bearing Capacity 3. Terzaghi’s Theory of Bearing Capacity 4. Skempton’s Theory of Bearing Capacity 5. Meyerhof’s Theory 6. Hansen’s Theory of Bearing Capacity 7. Vesic’s Theory of Bearing Capacity.

1. Rankine’s Theory of Bearing Capacity:

Rankine (1885) attempted to determine ultimate bearing capacity of the soil by considering the equilibrium of two elements of the soil, one below the footing and another outside the footing adjacent to the first element.

Following is the equation for ultimate bearing capacity as per Rankine’s theory for cohesionless soil:

where K_p is the Rankine’s coefficient of passive earth pressure.

As per Rankine’s theory, when the depth of foundation is zero, the ultimate bearing capacity is also zero, which is not true. As the Rankine’s theory does not give reliable value of ultimate bearing capacity, it is rarely used in practice. Instead, Rankine’s theory is used to determine the minimum depth of foundation as –

where K_a is the Rankine’s coefficient of active earth pressure and q the maximum pressure applied at the base of the foundation.

2. Prandtl’s Theory of Bearing Capacity:

Prandtl (1920) proposed his theory of bearing capacity based on his study of penetration or punching of long hard metal puncher into a softer material. While all modern theories of bearing capacity are based on Terzaghi’s theory, Terzaghi’s theory itself is based on Prandtl’s theory of bearing capacity.

Prandtl considered a strip footing with a smooth base that sinks vertically down when placed on a ground surface. Figure 18.1 shows the failure surface of the soil as per Prandtl’s theory. Prandtl has shown that when a continuous footing, with a smooth base, rests on a weightless soil possessing cohesion and friction angle, it sinks into the soil that fails by punching shear.

When the footing sinks, the wedge-shaped zone-I below the footing, pushes zone-II in the lateral direction, which in turn pushes zone-III in upward direction. Both zone-II and zone-III are in plastic equilibrium. By consid­ering the shape of failure surface of zone-II as logarithmic spiral, Prandtl gave the following equation for ultimate bearing capacity based on the theory of plasticity –

For a purely cohesive soil, ɸ_u = 0. The logarithmic spiral becomes a circular arc and the ultimate bearing capacity is given by –

q_u = (π + 2)c_u = 5.14c_u …(18.7)

Since the actual footings have a rough base, Prandtl’s theory does not give accurate results.

3. Terzaghi’s Theory of Bearing Capacity:

Terzaghi gave a general theory for the determination of ultimate bearing capacity of a strip footing. A strip foot­ing is a continuous footing provided to support the wall of a load bearing structure. The footing is assumed to be continuous with length-width ratio (L/B) more than 10, so that the problem is assumed to be two-dimensional. Terzaghi’s theory (1943) of bearing capacity is based on Prandtl’s theory (1921).

Failure Surface in Terzaghi’s Theory:

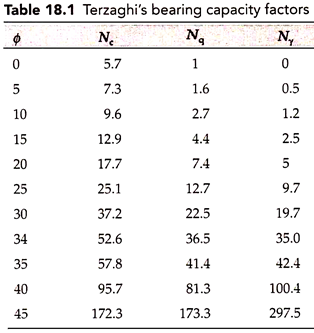
The base of the footing is assumed to be rough, unlike in Prandtl’s theory, so that a wedge-shaped mass of soil abc as shown in Fig. 18.2 does not undergo any lateral displacement and sinks vertically down, when the footing is subjected to the pressure q_u, equal to the ultimate bearing capacity of the soil.

The shape of elastic zone depends on the density and cohesion of the soil. The sides ca and cb rise at an angle ɸ with horizontal. The wedge of soil abc, known as zone-I, is in a state of elastic equilibrium and behaves as if it were a part of the footing.

Figure 18.2 shows the failure surface in Terzaghi’s theory, which does not extend above the base of the footing. Thus, Terzaghi neglected the shear strength of the soil above the base of the footing. Terzaghi considered the effect of the soil above the base of the footing in the form of a surcharge, γd_f, acting at the level of the base of the footing, where d_f is the depth of foundation. This assumption limits the applicability of Terzaghi’s theory to shallow foun­dations. For deep foundations, neglecting the shear strength of soil above the base of footing leads to serious errors.

The failure surface in Terzaghi’s theory consists of zone-II on the either side of zone-I and zone-Ill on the outer side of footing adjacent to zone-II. Zone-II is called the zone of radial shear. Sides ca and cb act as retaining walls pushing the soil in zone-II in the downward and outward direction. The bottom surface cd and cf of zone-II is a logarithmic spiral, with its center at points b and a, respectively, on the either side of the footing. Surfaces cd and cf can be defined by the equation –

r = r_0eθ ^tanɸ …(18.8)

where θ is the angle subtended at the center of any point on the spiral with the zero-angle radius vector cb or ca. Thus, the length of cb and ca is each equal to r₀.

Derivation of Terzaghi’s Bearing Capacity Equation:

The pushing of soil by the imaginary retaining walls cb and ca through zone-II, makes the soil in zone-Ill into pas­sive Rankine state. Sides db and de or fa and fg of zone-Ill rise at an angle (45 – ɸ/2) with the horizontal.

Terzaghi determined the ultimate bearing capacity of strip footing by considering the equilibrium of the wedge of soil abc (zone-I).

The forces acting on this wedge are as follows:

A. Upward Forces:

i. The resultant passive earth pressure, P_p, acting on the sides cb and ca at an angle ɸ with the normal to the surfaces cb and ca. Since the surfaces cb and ca are at an angle ɸ with horizontal, the direction of P_p is vertical.

ii. The cohesive force, C, acting along the sides cb and ca. The component of this cohesive force in vertical direction is equal to C sinɸ.

If c is the unit cohesion of soil, then –

C sinɸ = (c × ca sinɸ) + (c × cb sinɸ) …(18.9)

In Δabc (Fig. 18.3), we have ab = B and ah = B/2. So –

Substituting the values of ca and cb in Eq. (18.9), we get –

A. Downward Forces:

i. The force due to the pressure q_u acting vertically downward. Its magnitude is equal to q_uB per meter length of the footing.

ii. The weight of wedge of soil abc (zone-I) is –

W = γ × Area of Δabc × 1

In Δach (Fig. 18.3), ah = B/2. Hence –

tanɸ = ch/ah

Therefore, ch = ah and tanɸ = B/(2 tanɸ). So the area of Δabc will be –

½ × ab × ch = ½ × B × B/2 tanɸ = B²/4 tanɸ

Therefore,

W = γB²/4 tanɸ …(18.10)

The effect of surcharge γD and the weight of soil in zone-II and zone-III is taken into account in the computation of the passive earth pressure, P_p. Equating the downward and upward forces for equilibrium of the wedge abc we have –

q_uB + (γB²/4) tanɸ = 2P_p + Bc tanɸ …(18.11)

Therefore –

q_u B = 2P_p + Bc tanɸ – (γB²/4) tan ɸ …(18.12)

The resultant passive earth pressure P_p consists of the following three components:

a. P_pγ due to the weight of soil in zone-II and zone-III, assuming the soil as cohesionless and neglecting the sur­charge γD.

b. P_pc due to the cohesion of soil in zone-II and zone-Ill assuming the soil as weightless (γ = 0) and neglecting the surcharge γD.

c. P_pq due to the surcharge γD, assuming the soil as cohesionless and weightless.

Terzaghi assumed that these three components of P_p can be computed independently and added, though the critical surfaces for these components are different. Thus, Terzaghi assumed that the principle of superposition is valid. Substituting the three components of P_p in Eq. (18.12), we have –

Equation (18.22) is the famous Terzaghi’s bearing capacity equation for ultimate bearing capacity of strip footings. It is found to be applicable for strip footing with L/B ratio > 5.

Several theories of bearing capacity were developed later by taking into account the effect of shape and depth of footing, inclination of load or ground, etc. But the same form of the Terzaghi’s equation [Eq. (18.22)] was used by all the investigators, introducing additional factors to consider these effects. In spite of several theories coming up later, Terzaghi’s theory is still popular and is used as a simple solution to determine bearing capacity.

Terzaghi’s Bearing Capacity Factors:

Terzaghi found that bearing capacity factors N_c, N_q, and N_γ are functions of ɸ, the angle of shearing resistance of soil. The values of N_c, N_q and N_γ as given by Terzaghi are shown in Table 18.1.

Assumptions in Terzaghi’s Theory of Bearing Capacity:

The assumptions used for deriving the bearing capacity equation may be summarized as follows:

i. The soil mass is homogeneous and isotropic.

ii. The soil mass is semi-infinite, that is, it extends infinitely below a level surface.

iii. The footing is laid at a shallow depth, that is, D < B.

iv. The footing is continuous with L/B ratio > 10, so that the problem is essentially two-dimensional. Thus, Terzaghi considered plane strain condition, neglecting the effect of intermediate principal stress.

v. The base of the footing is rough.

vi. The failure surface does not extend above the base of the footing, that is, the shear strength of the soil above the base of the footing is neglected.

vii. The effect of soil above the base of the footing is considered in the form of surcharge, γD, acting at the level of the base of the footing.

viii. The load on the footing is vertical and its line of action coincides with the centroid of the footing.

ix. The shear strength of the soil is governed by Coulomb’s equation.

x. The principle of superposition is valid, so that the three components of the passive earth pressure can be com­puted separately and then added, although their critical surfaces are different.

Ultimate Bearing Capacity for Pure Cohesive Soils:

For pure cohesive soils, ɸ_u = 0 and Terzaghi’s bearing capacity factors are N_c = 5.7, N_q = 1; N_γ = 0; c = c_u. By Substituting these values in Eq. (18.22), the ultimate capacity of strip footing for pure clays is given by –

q_u = 5.7 c_u + γD …(18.23)

The net ultimate bearing capacity of strip footings for clays is, therefore, given by –

q_nu = 5.7 c_u …(18.24)

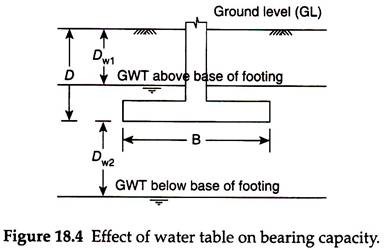
Effect of Water Table on Bearing Capacity:

Terzaghi’s theory of bearing capacity assumes that the groundwater table is at a great depth below the base of the foundation and hence its effect is not considered. When the groundwater table is near the level of the foundation, the unit weight of soil gets reduced. The effective or submerged unit weight of the soil shall be, therefore, used in the bearing capacity equation.

The effect of water table on the bearing capacity (Fig. 18.4) can be explained with reference to the bearing capac­ity equation [Eq. (18.22)] rewritten as –

q_u = cN_c + γDN_q + 0.5γBN_γ

The first term cN_c is not affected by the position of the water table, as it does not contain the density. However if the water table reaches the base of the footing, the unit cohesion c and the value of ɸ used to find N in the term should be determined in the laboratory under saturated conditions.

The second term γDN_q is contributed by the soil above the foundation level. Hence, this is not affected by the position of the water table, as long as the water table is at or below the base of the foundation. When the water table is at the GL, the term γDN_q gets reduced by about 50%, since for all practical purposes, the submerged density of the soil is about half of its saturated density. For any intermediate position of the water table, between the GL and the base of foundation, we may write the bearing capacity equation as –

where R_w1 is the water table correction factor, D_w1 is the depth of water table below GL, and D is the depth of foundation.

As per Eq. (18.26), when the water table is at GL, D_w1 = 0 and R_w1 = 0.5 and when the water table is at the base of the foundation, D_w1 = D and R_w1 = 1

The third term in the bearing capacity equation, that is, 0.5 γBN_γ, is contributed by the soil below the base of the foundation of depth approximately equal to the width of the foundation, where the stresses due to foundation load are significant. Thus, when the water table is at a depth greater than the width of the foundation below its base the term 0.5γBN_γ is not affected by the water table.

If the water table reaches the base of the foundation, the submerged density will be approximately half of the saturated density, reducing the term 0.5γBN_γ by about 50%. For any intermediate position of the water table, we may write the bearing capacity equation as –

where R_w2 is the water table correction factor, D_w2 is the depth of water table below the base of the foundation and B is the width of foundation.

When the water table is at the depth B below the base of the foundation, D_w2 = B and R_w2 = 1. When the water table is at the base of the foundation, D_w2 = 0 and R_w2 = 0.5.

If the water table is above the base of the foundation, the soil below the base of the foundation will be under submerged condition and hence D_w2 = 0 and R_w2 = 0.5

Terzaghi’s Bearing Capacity for Square, Circular and Rectangular Footings:

The bearing capacity equation for strip footings given by Terzaghi is modified for footings of other shapes. The ultimate bearing capacity of square footings is given as –

q_u = 1.2cN_c + γDN_q + 0.4γBN_γ …(18.29)

and the ultimate bearing capacity of circular footings will be –

q_u = 1.2 cN_c + γDN_q + 0.3γBN_γ …(18.30)

The ultimate bearing capacity of rectangular footing will be –

q_u = cN_cS_c + γDN_qS_q + 0.5γBN_γS_{γ .}..(18.31)

where S_c, S_q , and S_γ are the shape factors defined by the following equations –

It may be noted that for square footing, for which B = L, the shape factors are –

S_c = 1.2, S_q = 1, and S_γ = 0.8 …(18.34)

For circular footings, the shape factors used in the equation are –

S_c = 1.2, S_q = 1, and S_γ = 0.6 …(18.35)

Bearing Capacity for Pure Cohesive Soils for Square and Circular Footings:

For pure cohesive soils, ɸ_u = 0 and c = c_u and Terzaghi’s bearing capacity factors are N_c = 5.7, N_q = 1, and N_γ = 0. Hence, the net ultimate bearing capacity of square or circular footings for pure cohesive soils, as per Terzaghi’s theory is given by –

q_nu = 6.84c_u …(18.36)

4. Skempton’s Theory of Bearing Capacity:

For saturated cohesive soils, Skempton showed that the bearing capacity factor, N_c, in Terzaghi’s equation tends to increase with depth as shown in Fig. 18.9, where N_c increases with increase in D_f/B ratio.

The net ultimate bearing capacity for saturated cohesive soils under undrained conditions, as per Skempton’s theory is given by –

q_nu = c_uN_c …(18.40)

where q_nu is the net ultimate bearing capacity, c_u the undrained cohesion, N_c the Skempton’s bearing capacity factor given by Eqs. (18.41)-(18.44).

It may be noted that Terzaghi’s value of N_c is applicable only for shallow foundations with –

D_f/B < 1.0

whereas, Skempton’s value of N_c can be used for all values of D_f/B.

If the shear strength of the soil for a depth of 2B/3 beneath the footing does not vary by more than about ±50% of the average value, the average value of c_u can be used in the above equation for q_nu.

5. Meyerhof’s Theory:

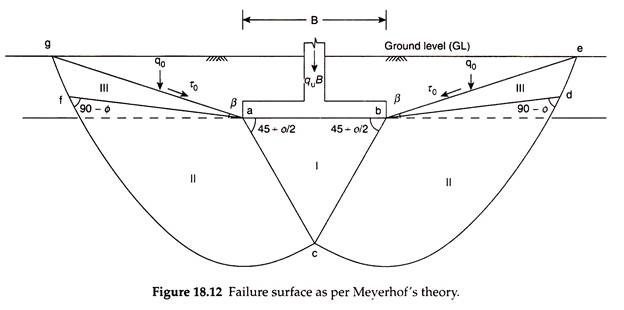
Meyerhof (1951) gave a general theory of bearing capacity for a strip footing at any depth. His equation is similar to that of Terzaghi, but his approach to solve the problem is different. He assumed that the logarithmic failure surface extends above the base of the foundation and as such considered the shear resistance of the soil above the base of the footing.

Figure 18.12 shows the failure surface as proposed by Meyerhof. The zone “abc” is the zone of elastic equi­librium with sides ac and be inclined at 45 + (ɸ/2) with horizontal. The zone bed is the zone of radial shear. The zone bed is the zone of mixed shear in which the shear varies from radial shear to linear shear. The surface be is known as equivalent free surface. It makes an angle β with the horizontal. The angle β increases with the depth D_f and is equal 90° for deep foundations. The resultant effect of the wedge bef of the soil is considered by the normal stress q₀ and the shear stress τ₀ on the surface be. The parameters β, q₀, and τ₀ are known as foundation depth parameters.

Meyerhof gave the following equation for ultimate bearing capacity –

where s, d, and i are the shape, depth, and inclination factors, respectively. N_c, N_q, and N_γ are the bearing capacity factors.

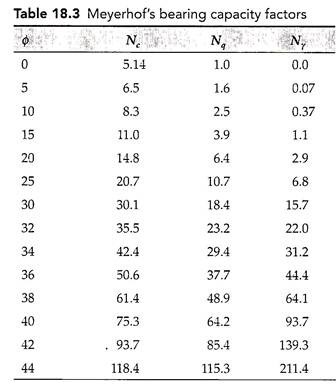
N_c, N_q, and N_γ depend on the roughness of the base of footing, shape of the footing in addition to D_f and ɸ. Table 18.3 gives the Meyerhof’s bearing capacity factors for different values of ɸ.

The ultimate bearing capacity, given by Meyerhof’s theory, is close to the experimental values. For shallow footings, the Meyerhof’s bearing capacity lies in between the general and local shear values of Terzaghi’s analysis. However, for deep footings, Meyerhof’s analysis gives values much greater than those given by Terzaghi’s analysis. The main advantage of Meyerhof’s theory is that it can also be used for deep foundations as well as for footings on slopes.

Meyerhof introduced the concept of effective width to compute bearing capacity for eccentrically loaded foot­ings. For strip footing –

B’ = B – 2e_x …(18.49)

For rectangular footing –

B’ = B – 2e_x …(18.50)

L’ = L – 2e_y ….(18.51)

where B’ is the effective width of footing in the X-direction and L’ is the effective length of footing in the Y-direction.

The shape, depth, and inclination factors in Meyerhof’s bearing capacity equation are as follows –

Shape factors –

where α is the angle of inclination of load with vertical.

Meyerhof recommended the use of ɸ_r in place of ɸ for strip footings and rectangular footings under a plane strain condition.

where ɸ_r is the angle of shearing resistance under a plane strain condition to be used for computation of bearing capacity and ɸ the angle of shearing resistance obtained from triaxial compression tests.

6. Hansen’s Theory of Bearing Capacity:

Brinch Hansen (1970) extended Meyerhof’s theory to determine the bearing capacity for footings with an inclined base and for footings with sloping ground surface. Hansen, Vesic, and Prandtl computed bearing capacity assum­ing the base of the footing as smooth.

Hansen introduced the base inclination and ground surface inclination factors in Meyerhof’s bearing capacity equation and proposed the following equation for bearing capacity –

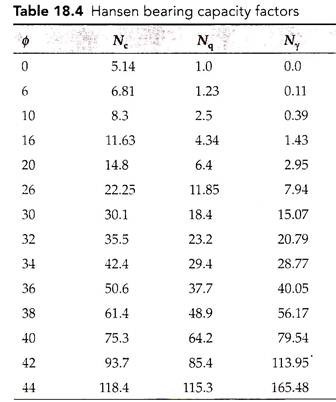
Table 18.4 gives the bearing capacity factors proposed by Hansen. It may be noted that N_c and N_q factors given by Hansen are the same as those given by Meyerhof. The shape, depth, and inclination factors proposed by Hansen are functions of not only B/L and D/B but also of other factors such as N_c, N_q, ɸ, and many others. Computation of bear­ing capacity by Hansen’s theory is more complicated than that by other theories.

It was observed that Terzaghi’s theory gives conservative values of bearing capacity for cohesionless soils, while the values obtained for cohesive soils from the equations are more than those given by experimental results. Bearing capacity values as obtained by Hansen’s theory for cohesive soils are in better agreement with experimental results on model footings.

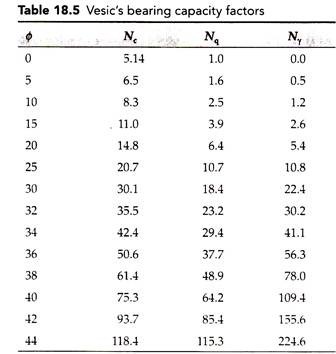
7. Vesic’s Theory of Bearing Capacity:

Vesic (1973) used the failure surface similar to that used in Terzaghi’s theory, except that the slope of elastic wedge (zone-I) is assumed to be (45 + ɸ/2) with horizontal. He used the same form of equation as used by Hansen but modified some of the A factors, while adopting the other A factors from Hansen’s theory, as shown below –

The bearing capacity factors N_q and N_c suggested by Vesic are the same as those given by Hansen. Vesic gave a slightly modified equation for N_y, that is –

Table 18.5 gives the bearing capacity factors proposed by Vesic.

The value of N_c and N_q computed by different methods will be more or less same, and the difference between different theories of bearing capacity lies only in the value of N_γ as –

N_γ = (N_q – 1) tan (1.4ɸ) Meyerhof

N_γ = 1.5(N_q – 1) tanɸ Hansen

N_γ = 2(N_q – 1) tanɸ Vesic