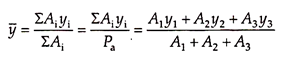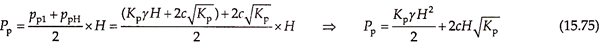Rankine’s Theory of Passive Earth Pressure | Soil

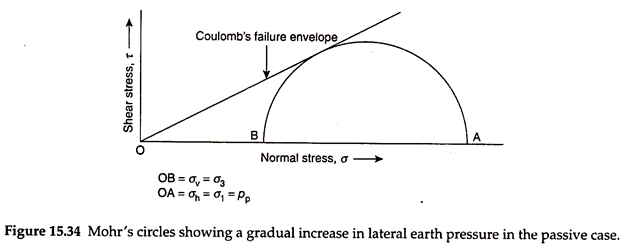
In the passive case, the retaining wall moves toward the soil, causing compression of the soil and increasing the lat­eral earth pressure. When the soil reaches the state of plastic equilibrium, the Mohr’s circle touches the Coulomb’s failure envelope. Thus, in the passive case, the vertical stress is more than the horizontal stress, since both the stresses are considered as principal stresses.

Dry Cohesionless Backfill:

In passive case, we know that –

Major principal stress, σ₁ = p_p and minor principal stress, σ ₃ = σ _v = γh

Figure 15.34 shows the Mohr’s circle of stresses and the failure envelope for the passive case. When the soil element reaches the state of plastic equilibrium with sufficient movement of the wall toward the soil, the Mohr’s circle of stresses touches the Coulomb’s failure envelope, as shown in Fig. 15.34.

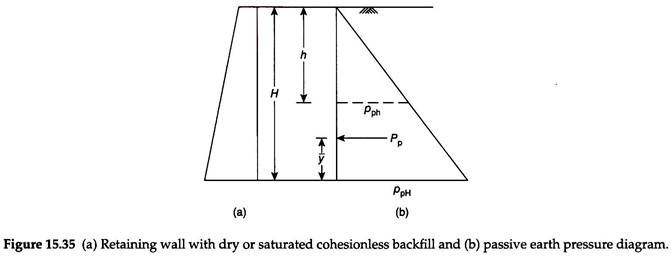
Figure 15.35(a) shows a retaining wall in which a soil element at any depth h is considered. We know that the principal stresses are related to the shear parameters of the backfill material by the Bell’s equation, restated as –

σ₁ = σ₃ tan² α + 2c tan α …(15.56)

Considering a dry cohesionless backfill, we have –

c = 0; σ₁ = p_p; σ₃ = σ_v = γh

Substituting these values in Eq. (15.56), we have –

p_p = γh tan² α + 0 ⇒ p_p = γh tan² α = K_pγh …(15.57)

where K_p the Rankine’s coefficient of passive earth pressure, is given by –

K_p = tan² α = (1 + sinɸ)/(1 – sinɸ) …(15.58)

α = 45 + ɸ/2

Equation (15.57) indicates that the passive earth pressure is zero at the top surface of the backfill (h = 0) and increases linearly with depth below the surface. The distribution of passive earth pressure is shown in Fig. 15.35(b).

The total or resultant passive earth pressure exerted on the wall is obtained by computing the area of the pres­sure diagram.

Total active earth pressure = Area of the pressure diagram

that is –

The total active earth pressure acts horizontally through the centroid of the pressure diagram. Vertical distance of total active earth pressure above the base of the wall = y̅.

For a triangular pressure distribution, we know that y̅ = (H/3) above the base of the wall. The failure plane makes an angle of α = 45 + (ɸ/2) with the major principal plane. As the major principal stress in the passive case is horizontal, the major principal plane is vertical and the failure plane makes an angle of α = 45 – (ɸ/2) with the horizontal.

Fully Submerged Cohesionless Backfill:

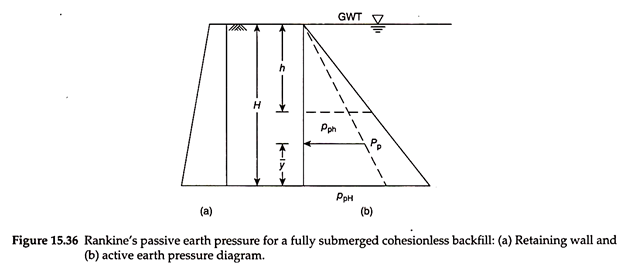
Figure 15.36(a) shows a retaining wall with a fully submerged backfill, with the groundwater table at the surface of the backfill. The principle of determination of passive earth pressure is to multiply the effective vertical stress with the lateral pressure coefficient (K_p) and then add the hydrostatic pressure due to the water table, if any. This is because the hydrostatic pressure is equal in all directions as per Pascal’s law, and hence, lateral pressure coefficient (K_p) should not be applied to the hydrostatic pressure.

The active earth pressure at any depth h below the surface of the backfill, as per Rankine’s theory, is given by –

p_p = K_pγ’ h + γ_w h …(15.60)

where –

K_p = (1 + sinɸ) / (1 – sinɸ)

Here γ’ is the submerged density of the backfill material and γ_w, the density of water, is 9.81 kN/m³ = 1 t/m³= 1 g/cc.

The passive earth pressure at the base of the wall –

p_pH = K_pγ’ H + γ_wH …(15.61)

Figure 15.36(b) shows the passive earth pressure diagram. The total or resultant active earth pressure exerted on the wall is obtained by computing the area of the pressure diagram.

Total active earth pressure = Area of the pressure diagram

that is –

The total active earth pressure acts horizontally through the centroid of the pressure diagram. Vertical distance of total active earth pressure above the base of the wall = y̅. For a triangular pressure distribution, we know that y̅ = (H/3) above the base of the wall.

Partially Submerged Cohesionless Backfill:

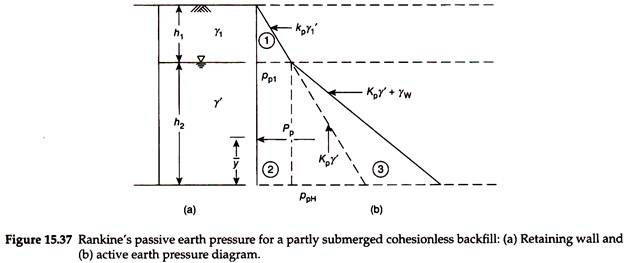
Figure 15.37(a) shows a retaining wall of height H, with a partially submerged backfill, with the groundwater table at a depth h₁ below the surface of the backfill. The soil above the water table may be either partially or fully satu­rated. The bulk density of the soil is to be used for the computation of the vertical stress for soil above the water table.

The active earth pressure at depth h₁ below the surface of the backfill is given by –

p_p1 = K_pγh₁ …(15.62)

The active earth pressure at the base of the wall is given by –

P_pH = K_Pγh₁ + K_pγ’h ₂ + γ_wh₂ …(15.63)

Figure 15.37(b) shows the passive earth pressure diagram. Due to the use of submerged density, the slope of the pressure diagram (K_aγ’) decreases below the water table (dotted line) as compared with that (K_aγ) above the water table. As the water pressure is added, the slope of the active pressure diagram (K_aγ’ + γ_w) is more than that above the water table (solid line). The total or resultant active earth pressure exerted on the wall is obtained by computing the area of the pressure diagram, that is –

Total active earth pressure = Area of the pressure diagram ⇒ P_p = A = A₁ + A₂ + A₃

The total active earth pressure acts horizontally through the centroid of the pressure diagram. Vertical distance of the total active earth pressure above the base of the wall is y̅. The distance of centroid can be computed from the principles of mechanics using Eq. (15.21) –

where y̅ is the distance of the line of action of P_a above the base of the wall, A₁, A₂, A₃ are the areas of segments 1, 2, and 3 of the pressure diagram as shown in Fig. 15.37(b), and y₁, y₂, y₃ are the distances of the centroid of segments 1, 2, and 3 from the base of the wall.

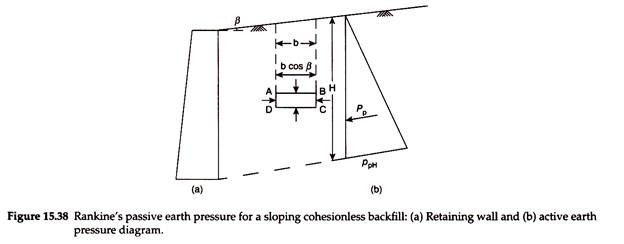
Cohesionless Backfill with Sloping Surface:

Figure 15.38(a) shows a retaining wall with a cohesionless backfill having its surface sloping at an angle βwith the horizontal.

Consider an element of width b, along the slope, at any depth h below the surface of the backfill.

Rankine con­sidered that the soil element is subjected to two stresses:

i. Vertical stress, σ_v, due to self-weight of the soil, acting vertically downward on the inclined planes AB and CD of the soil element.

ii. Passive earth pressure, p_p, acting parallel to the surface of the backfill on the vertical planes BC and AD.

The two stresses are called conjugate stresses because the direction of each stress is parallel to the plane on which the other stress is acting. As shear stress also acts on plane AB of the soil element, the vertical stress is not a princi­pal stress. Similarly, the lateral pressure is also not a principal stress. Volume of the soil above the element per unit length –

V = h × b cos β x 1 = bh cos β

Weight of the soil above the element –

W = γ × V = γ × (bh cos β)

Resisting area of the soil element –

A = b × 1 = b

Vertical stress on the soil element –

σ_v = (W/A) = {[γ × (bh cosβ)]/b} = γh cosβ .

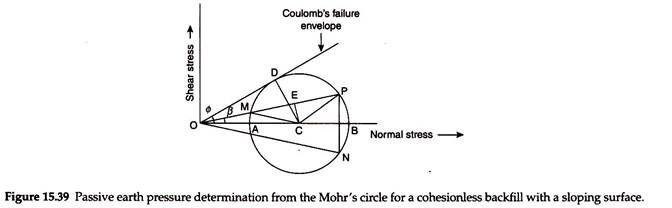
Figure 15.39 shows the Mohr’s circle of stresses for the soil element. Point M represents plane AB, and hence, OM gives the vertical stress. When the backfill is in plastic equilibrium, the Mohr’s circle passes through point M and will be tangential to the Coulomb’s failure envelope.

To find pole P on the Mohr’s circle, a line is drawn from point M parallel to plane AB (on which it is acting) to intersect the Mohr’s circle at point P, as shown in Fig. 15.39. Now from point P, a line is drawn parallel to plane AD (on which p_p is acting) to intersect the Mohr’s circle at point N. Point N represents plane AD on which the passive earth pressure p_p is acting. Hence, ON gives the value of p_p –

(P_p/σ_v) = (ON/OM) = (OP/OM) = [(OE + EP)/(OE-EM)]

which is the same as Eq. (15.58) for a cohesionless backfill with a horizontal surface. It should be noted that passive earth pressure is assumed to act at an angle β with the horizontal parallel to the backfill surface. Equation (15.67) indicates that passive earth pressure is zero at the top surface of the backfill (h = 0) arid increases linearly with depth below the surface. Passive earth pressure at the base of the wall,

p_pH = K_pγH …(15.69)

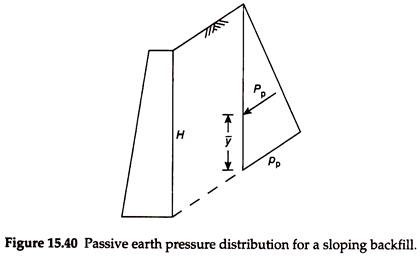
The distribution of passive earth pressure is shown in Fig. 15.40. The total or resultant passive earth pressure exerted on the wall is obtained by computing the area of the pressure diagram.

Total passive earth pressure = Area of the pressure diagram ⇒ P_p = A = ½ × p_pH × H = ½ × K_pγH ×H

that is –

P_p = K_pγH²/2 …(15.70)

The total passive earth pressure acts at an angle β with the horizontal through the centroid of the pressure diagram. Vertical distance of the line of action of total passive earth pressure above the base of the wall = y̅.

For a triangular pressure distribution, we know that y̅ = (H/3) above the base of the wall. It must be noted that the generation of passive earth pressure is possible only if the retaining wall is pushed towards the backfill.

Rankine’s Passive Earth Pressure for Cohesive Backfill:

We know that the principal stresses are related to soil properties by Bell’s equation, which is restated –

σ = σ₃ tan² α + 2c tan α …(15.71)

In the passive case –

Major principal stress, σ₁ = p_p and minor principal stress, σ₃ = σ_v = γh

Substituting these in Eq. (15.71), we have –

p_p = σ_v tan² α + 2 c tan α = γh tan² α + 2c tan α ⇒ p_p = K_pγh + 2c √K_p …(15.72)

where –

K_a = tan² α = (1 + sinɸ)/ (1 – sinɸ)

When h = 0

p_p1 = 2c√K_p …(15.73)

When h = H

P_pH = K_pγH + 2c √K_p …(15.74)

Thus, unlike the active case, there is no negative pressure in the passive case. The total passive earth pressure can be obtained by computing the area of the pressure diagram, which is trapezoidal –

The total passive earth pressure acts horizontally through the centroid of the pressure diagram. Vertical distance of the total active earth pressure above the base of the wall = y̅. For a trapezoidal pressure distribution, we know that the distance of the centroid above the base of the wall –