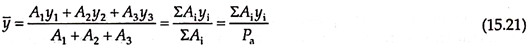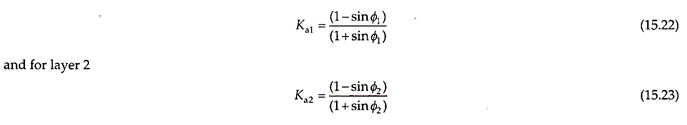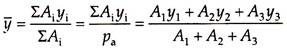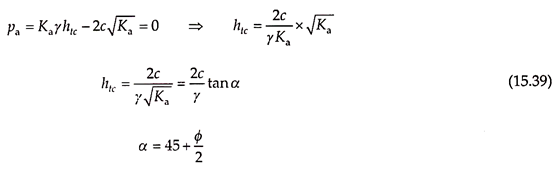Rankine’s Theory of Active Earth Pressure | Soil

Rankine (1857) considered the equilibrium of a soil element at any depth (h) in the backfill behind a retaining wall and determined the active earth pressure.

Rankine assumed that the soil element is subjected to only two types of stresses:

i. Vertical stress (σ_z) due to the weight of the soil above the element.

ii. Lateral earth pressure (p_a).

Dry Cohesionless Backfill:

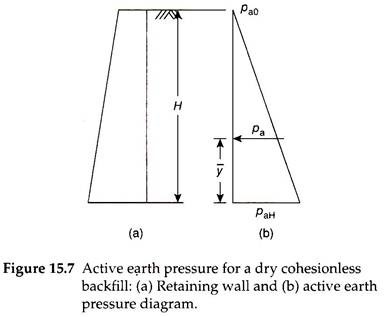
Assuming the back of the wall as smooth and vertical, Rankine considered that the active earth pressure (p_a) acts horizontally for a backfill with a horizontal surface [Fig. 15.7(a)]. In the active case, the vertical stress is more than the horizontal stress. Since both the stresses are considered as principal stresses –

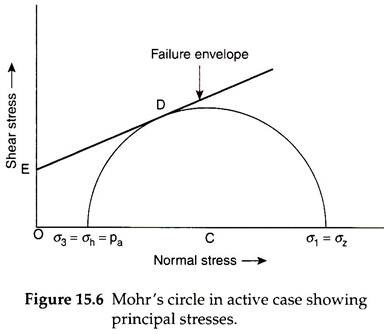
Major principal stress, σ₁ = σ_z = γh and minor principal stress, σ₃ = p_a

Figure 15.6 shows the Mohr’s circle of stresses and the failure envelope for the active case. When the soil element reaches the state of plastic equilibrium with sufficient movement of the wall away from the backfill, the Mohr’s circle of stresses touches the Coulomb’s failure envelope, as shown in Fig. 15.6.

It is known that the principal stresses are related to the shear parameters of the backfill material by the Bell’s equation as follows –

σ₁ = σ₃ tan² α + 2c tan α …(15.7)

Considering a dry cohesionless backfill, we have c = 0, hence –

σ₁ = σ_z = γh (in active case) and σ₃ = p_a

Substituting these values in Eq. (15.7), we have –

where K_a is the Rankine’s coefficient of active earth pressure and is given by –

α = 45+ ɸ/2

Equation (15.8) indicates that the active earth pressure is zero at the top surface of the backfill (h = 0) and increases linearly with depth below the surface. The distribution of active earth pressure is shown in Fig. 15.7(b).

The total or resultant active earth pressure exerted on the wall is obtained by computing the area of the pressure diagram.

Total active earth pressure = Area of the pressure diagram

that is,

The total active earth pressure acts horizontally through the centroid of the pressure diagram. Vertical distance of total active earth pressure above the base of the wall = y̅.

For a triangular pressure distribution, we know that y̅ = (H/3) above the base of the wall. The failure plane makes an angle of α = 45 + (ɸ/2) with the major principal plane. As the major principal stress in the active case is vertical, the major principal plane is horizontal and the failure plane makes an angle of α = 45 + (ɸ/2) with the horizontal.

The assumptions made in Rankine’s theory of earth pressure may be summarized as follows:

i. The backfill is homogeneous and semi-infinite.

ii. The backfill is dry and cohesionless.

iii. The surface of the backfill is plane and horizontal.

iv. The back of the retaining wall is vertical and smooth so that there is no friction between the wall and the backfill when the wall moves away from the backfill.

v. The shear strength of the backfill is governed by Coulomb’s equation.

vi. The wall moves sufficiently away from the backfill so that the Mohr’s circle touches the failure envelope and the backfill attains a state of plastic equilibrium so that lateral earth pressure becomes minimum equal to active earth pressure.

vii. The position and direction of the resultant or total active earth pressure are known. The resultant active pressure acts parallel to the surface of the backfill through the centroid of the pressure diagram.

Cohesionless Backfill with Surcharge:

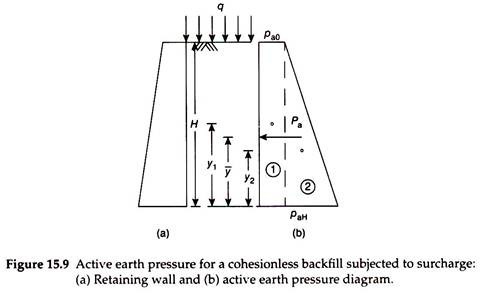
Figure 15.9(a) shows a retaining wall with a horizontal backfill subjected to additional pressure (surcharge) of inten­sity q (kN/m²) on the backfill surface. The surcharge applied at the top may be assumed to be uniform throughout the depth of the wall. The simple principle for the determination of active earth pressure at any level in Rankine’s theory is to multiply the vertical stress at that depth with the Rankine’s coefficient of active earth pressure. Vertical stress at any depth below the top of the backfill –

σ_v = γh + q …(15.12)

Hence, active earth pressure at any depth is given by –

p_a = K_a σ_v = K_a(γh + q) ⇒ p_a = K_aγh + K_aq …(15.13)

When h = 0, active earth pressure at the top of the backfill is given by –

p_a0 = K_a × γ × 0 + K_aq = K_aq

When h = H, active earth pressure at the bottom of the wall is given by –

P_aH = K_a × γ × H + K_aq = K_aγH + K_aq

Thus, for a backfill subjected to a surcharge q at the top, the active earth pressure distribution is trapezoidal, as shown in Fig. 15.9(b), with intensity p_a0 at top and p_aH at bottom.

Total active earth pressure is obtained by computing the area of the pressure diagram –

P_a = (K_aq) × H + 1/2 × (K_aγH) × H ⇒ P_a = K_aqH + K_ayH²/2 …(15.14)

Total active earth pressure acts horizontally through the centroid of the pressure diagram. From the principles of mechanics, the distance of the centroid above the base of the wall is given by –

y̅ = ΣA_iy_i/ΣA_i …(15.15)

where A_i is the area of each part of the pressure diagram, that is, A₁ and A₂ and y_i the distance of the centroid of each part of the pressure diagram above the base of the wall, that is, y₁ and y₂.

The above principle of determination of active earth pressure when the backfill is subjected to a surcharge of intensity q may be similarly applied for determination of active or passive earth pressure under any backfill con­dition when the backfill is subjected to a surcharge. For example, passive earth pressure due to surcharge will be equal to K_pq.

Fully Submerged Cohesionless Backfill:

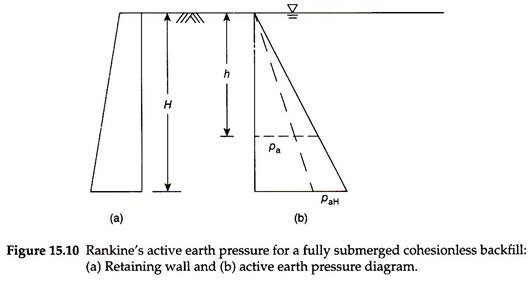
Figure 15.10(a) shows a retaining wall with a fully submerged backfill, with the groundwater table at the surface of the backfill. The principle of determination of active earth pressure is to multiply the effective vertical stress with the lateral pressure coefficient (K_a) and then add the hydrostatic pressure due to water table, if any. This is because the hydrostatic pressure is equal in all directions as per Pascal’s law, and hence, the lateral pressure coefficient (K_a) should not be applied to the hydrostatic pressure.

The active earth pressure at any depth h below the surface of the backfill, as per Rankine’s theory, is given by –

p_a = K_a γ’h + γ_w h …(15.16)

where K_a, the Rankine’s coefficient of active earth pressure, is –

K = (1 – sin ɸ)/(1 + sin ɸ)

Here γ’ is the submerged density of backfill material and γ_w the density of water is 9.81 kN/m³ = 1 t/m³= 1 g/cc. The active earth pressure at the base of the wall is –

P_aH = K_a γ’H ₊ γ_wH

Figure 15.10(b) shows the active earth pressure distribution program. Total or resultant active earth pressure exerted on the wall is obtained by computing the area of the pressure diagram. That is –

Total active earth pressure = Area of the pressure diagram

Total active earth pressure acts horizontally through the centroid of the pressure diagram. The vertical distance of total active earth pressure above the base of the wall = y̅.

For a triangular pressure distribution, we know that y̅ = H/3 above the base of the wall.

Partially Submerged Cohesionless Backfill:

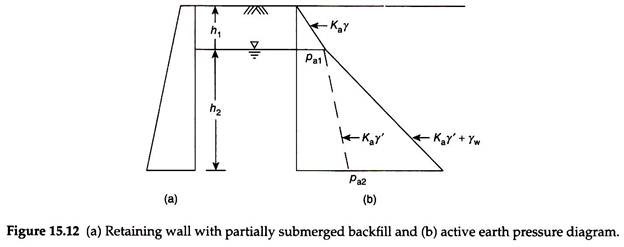
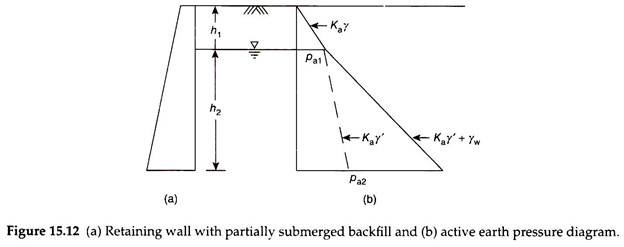
Figure 15.12(a) shows a retaining wall of height H, with a partially submerged backfill, with the groundwater table at a depth h₁ below the surface of the backfill. The soil above the water table may be either partially or fully saturated. The bulk density of the soil is to be used for computation of vertical stress for soil above the water table.

The active earth pressure at depth h₁ below the surface of the backfill is given by –

p_a1 = K_a γh₁ …(15.18)

where

K_a = (1 – sin ɸ)/(1 + sin ɸ)

where γ is the bulk density of the backfill material above the water table, γ’ the submerged density of the backfill material, and γ_w the density of water is 9.81 kN/m³ = 1 t/m³= 1 g/cc.

The active earth pressure at the base of the wall is given by –

P_a2 = K_aγh₁+K_aγ’h₂ + γ_wh₂ …(15.19)

Figure 15.12(b) shows the active earth pressure diagram. Due to the use of submerged density, the slope of the pressure diagram (K_aγ’) decreases below the water table (dotted line) as compared with that (K_aγ) above the water table. As the water pressure is added, the slope of the active pressure diagram (K_aγ’ + γ_w) is more than that above the water table (solid line). The total or resultant active earth pressure exerted on the wall is obtained by computing the area of the pressure diagram. That is –

Total active earth pressure = Area of the pressure diagram

Total active earth pressure acts horizontally through the centroid of the pressure diagram. Vertical distance of total active earth pressure above the base of the wall is y̅. The distance of the centroid can be computed from the prin­ciples of mechanics using –

where y̅ is the distance of line of action of P_a above the base of the wall, A₁, A₂, A₃ are the areas of segments 1, 2, and 3 of the pressure diagram as shown in Fig. 15.12(b), and y₁, y₂, y₃ the distances of the centroid of segments 1, 2, and 3 from the base of the wall.

Two-Layered Cohesionless Backfill:

Figure 15.15(a) shows a retaining wall of height H, with a cohesionless backfill of two layers having density of γ₁and γ₂, friction angles of ɸ₁ and ɸ₂ over depths h₁ and h₂, respectively. As the friction angles are different for each layer, the Rankine’s coefficient of active earth pressure will be different for the two layers. Thus, for layer 1 –

Active earth pressure at any level is obtained by multiplying the effective vertical stress at that level with the coefficient of active earth pressure at that level. Thus, active earth pressure in layer 1 at depth h₁ is given by –

P_a11 = K_a1γ₁h₁ …(15.24)

Active earth pressure in layer 2 at the same depth h₁ is given by –

P_a21 = K_a2γ₁h₁ …(15.25)

Active earth pressure at the base of the wall is given by –

P_a22 = K_a2(γ₁h₁ + γ₂h₂) …(15.26)

Figure 15.15(b) shows the active earth pressure diagram.

The total or resultant active earth pressure exerted on the wall is obtained by computing the area of the pressure diagram.

Total active earth pressure = Area of the pressure diagram

that is –

Total active earth pressure acts horizontally through the centroid of the pressure diagram. Vertical distance of total active earth pressure above the base of the wall = y̅. The distance of the centroid can be computed from the princi­ples of mechanics using Eq. (15.21) as –

where y̅ is the distance of line of action of p_a above the base of the wall, A₁, A₂, A₃ are the areas of segments 1, 2, and 3 of the pressure diagram as shown in Fig. 15.15, and y₁, y₂, y₃ are the distances of the centroid of segments 1, 2, and 3 from the base of the wall.

Cohesionless Backfill with Sloping Surface:

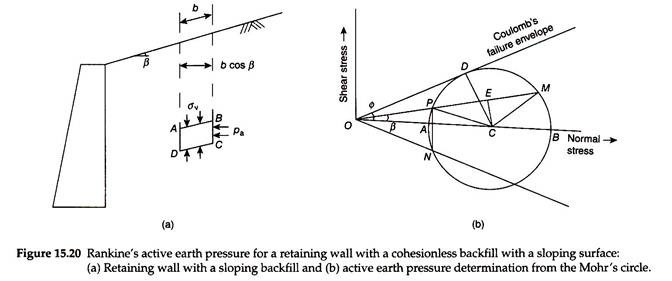
Figure 15.20(a) shows a retaining wall with a cohesionless backfill having its surface sloping at an angle β with the horizontal.

Consider a soil element of width b, along the slope, at any depth h below the surface of the backfill.

Rankine considered that the soil element is subjected to two stresses:

1. Vertical stress, σ_v, due to self-weight of the soil, acting vertically downward on the inclined planes AB and CD of the soil element.

2. Active earth pressure, p_a, acting parallel to the surface of the backfill on the vertical planes BC and AD.

The two stresses are called conjugate stresses because the direction of each stress is parallel to the plane on which the other stress is acting. As shear stress also acts on plane AB of the soil element, the vertical stress is not a principal stress. Similarly, lateral pressure is also not a principal stress. Volume of the soil above the element per unit length will be –

V = h × b cos β × 1 = bh cos β

Weight of the soil above the element will be –

W = γ × V = γ × (bh cos β)

Resisting area of the soil element will be –

A = b × 1 = b

Vertical stress on the soil element will be –

σ_v = W/A = γ × (bh cos β)/b = γh cos β

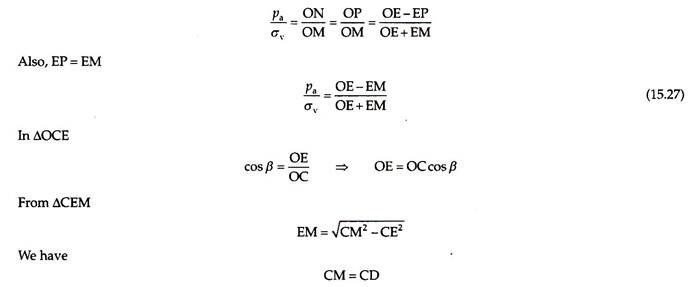
Figure 15.20(b) shows the Mohr’s circle of stresses for the soil element. Point M represents plane AB, and hence, OM gives the vertical stress. In fact, the vertical stress is the resultant of the normal stress and the shear stress acting on plane AB. When the backfill is in plastic equilibrium, the Mohr’s circle passes through point M and will be tangen­tial to the Coulomb’s failure envelope. To find pole P on the Mohr’s circle, a line is drawn from point M parallel to plane AB (on which it is acting) to intersect the Mohr’s circle at point P, as shown in Fig. 15.20(b).

Now from point P, a line is drawn parallel to plane AD (on which p_a is acting) to intersect the Mohr’s circle at point N. Point N represents plane AD on which the active earth pressure p_a is acting. Hence, ON gives the value of p_a.

It should be noted that active earth pressure is assumed to act at an angle P with the horizontal, parallel to the back­fill surface. If β = 0 is substituted in Eq. (15.30)

K _a = (1 – sin ɸ) (1 + sin ɸ)

which is the same as Eq. (15.9) for a cohesionless backfill with a horizontal surface.

Equation (15.29) indicates that active earth pressure is zero at the top surface of the backfill (h = 0) and increases linearly with depth below the surface. Active earth pressure at the base of the wall –

P_aH = K_a γH …(15.31)

The distribution of active earth pressure is shown in Fig. 15.21(b) for the wall with inclined backfill shown in Figs. 15.20 and 15.21(a).

The total or resultant active earth pressure exerted on the wall is obtained by computing the area of the pressure diagram.

Total active earth pressure = Area of the pressure diagram

that is –

The total active earth pressure acts at an angle β with the horizontal through the centroid of the pressure diagram. Vertical distance of the line of action of total active earth pressure above the base of the wall is y̅.

For a triangular pressure distribution, we know that y̅ = (H/3) above the base of the wall. The failure plane makes an angle of α = 45+ (ɸ/2) with the major principal plane. However, the major principal plane is not horizontal as in other active cases.

Let θ₁ is the angle of the major principal plane with the horizontal and θ_f is the angle of the failure plane with the horizontal –

θ_f = α – θ₁ …(15.32)

In ΔOCP, the exterior angle, Ψ = 2θ₁ + β, therefore –

θ₁ = (Ψ – β)/2

Substituting the value of θ₁ in Eq. (15.32), we have –

θ_f = α – [(Ψ – β)/2] …(15.33)

In ΔCEP,

The angle of the failure plane with the horizontal, θ_f, can be obtained by solving Eqs. (15.33) and (15.34) simultaneously.

Rankine’s Active Earth Pressure for Cohesive Backfill:

Resal (1910) and Bell (1915) extended Rankine’s theory of earth pressure for cohesive soils. We know that the principal stresses are related to soil properties by Bell’s equation, which is as follows –

σ₁ = σ₃ tan² α + 2c tan α …(15.35)

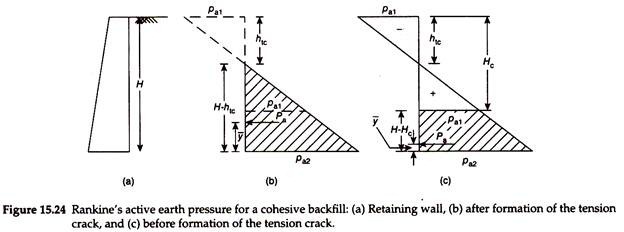
Consider a soil element at any depth h below the surface of the backfill, as shown in Fig. 15.24(a). In the active case, major principal stress –

σ₁ = σ_v = γh

Minor principal stress –

σ₃ = P_a

Substituting these in Eq. (15.35), we have –

σ_v = p_a tan² α + 2c tan α = γh ⇒ p_a tan² α = γh – 2c tan α

Thus, active earth pressure is negative at the top of the wall and increases linearly with the increase in depth. As the soil is weak in tension, tension cracks will develop in the negative active earth pressure zone of the backfill. The depth of a tension crack can be obtained by substituting p_a = 0 in Eq. (15.38) –

If the soil is able to withstand the negative active earth pressure, the negative pressure over the depth h_tc is balanced by a positive pressure over the same depth below. Hence, the resultant active earth pressure is zero over the depth H_c = 2h_tc, known as critical height. Thus, excavations in cohesive soils can stand with vertical sides without any lateral support over the critical height, provided no tension crack is developed in the negative pressure zone. Critical height –

The total active earth pressure can be obtained by computing the area of the pressure diagram.

The magnitude of total active earth pressure depends on whether a tension crack is developed in the negative pressure zone as shown below:

Case 1 – Active Earth Pressure When Tension Crack Is Developed:

Figure 15.24(a) shows a retaining wall of height H with a cohesive backfill. Figure 15.24(b) shows the active earth pressure diagram when a tension crack is formed. If a tension crack is developed, it indicates that the soil has failed in the negative pressure zone and hence the negative pressure will no longer be acting on the wall. The total active earth pressure is obtained by computing the area of the positive pressure diagram, ignoring the negative active earth pressure as shown in Fig. 15.24(b). That is –

Total active earth pressure = Area of the positive pressure diagram

The total active earth pressure acts horizontally through the centroid of the resultant pressure diagram. The height of the total active earth pressure above the base of the wall –

y̅ = (H – h_tc)/3 …(15.42)

Case 2 – Active Earth Pressure When Tension Crack is not developed:

If a tension crack is not developed, the negative pressure over the depth h_tc is balanced by a positive pressure over the same depth below. The wall will be therefore subjected to the net active earth pressure (shown hatched in Fig. 15.24(c)) below the critical height H_c. The depth of the wall, over which the net pressure acts, is (H – H_c).

The total active earth pressure is obtained by computing the area of the resultant pressure diagram over this depth, as shown hatched in Fig. 15.24(c). That is –

Total active earth pressure = Area of the resultant pressure diagram

The total active earth pressure acts horizontally through the centroid of the resultant pressure diagram. The height of the total active earth pressure above the base of the wall –

y̅ = (H – H_c)/3 …(15.44)