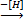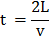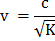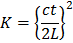Three-Dimensional Consolidation of Soil | Soil Engineering

Terzaghi’s theory of consolidation assumes that the expulsion of pore water during consolidation takes place in ver­tical direction alone. This is generally true for most of the cases, where the pervious layers, which form the drainage faces, are horizontal, located above and /or below the compressible soil layer. In some special cases, where vertical sand drains or sand wicks are installed to accelerate the consolidation of a natural or man-made fill, the compress­ible soil layer is surrounded by vertical drainage face, facilitating the pore water flow in horizontal direction from the stressed zone of compressible soil.

In such cases, where horizontal flow of pore water takes place, Terzaghi’s 1D theory of consolidation grossly underestimates the rate of consolidation. This is because the time required for dissipation of pore water pressure reduces because of additional flow in horizontal (lateral) direction and it is also because the permeability of soils in horizontal direction is several times (up to 25 times or more) more than that in vertical direction. For such cases, it is necessary to consider the flow in all directions to estimate the rate of consolidation.

1. Three-Dimensional Consolidation Equation in Cartesian Coordinates:

Consider the flow that is taking place through a small soil element of dimensions dx, dy, and dz in x, y, and z coordi­nate directions, respectively, as shown in Fig. 11.31. Let v_x be the velocity of pore water entering the soil element in X-direction, v_y be the velocity of pore water entering the soil element in Y-direction, and v_z be the velocity of pore water entering the soil element in Z-direction.

Then the velocity of pore water leaving the soil element –

in X-direction = v_x + (∂v_x/∂x) x dx

in Y-direction = v_y + (∂v_y/∂y) x dy

in Z-direction = v_z + (∂v_z/∂z) x dz

We know that the rate of flow (i.e., volume per unit time) of pore water is given by q = v x A, where v is the velocity of flow and A is the area of flow. Hence, the total volume of water entering the soil element per unit time is –

q_i = v_x x dy x dz + v_y x dz x dx + v_z x dx x dy

Volume of the water leaving the soil element per unit time is –

Volume of pore water squeezed (expelled) out of the element per unit time is –

where V₁ the initial volume = dx x dy x dz. From Eq. (11.22), we have –

Since the permeability of soil is not identical in x-, y-, and z-directions –

where k_z is the permeability of soil in z-direction. Similarly –

where k_x is the permeability of soil in x-direction and k_y the permeability of soil in the y-direction. Substituting the value of dvjdx, dv_y/dy, and dvjdz in Eq. (11.56), we have –

Assuming the soil to be homogeneous, density of water (γ_w) is uniform in all directions, while permeability (k) is uniform in the respective coordinate direction –

From the definition of coefficient of volume compressibility [Eq. (11.8)], we have –

m_v = –ΔV/V₁ x 1/Δσ’

Change in the volume of soil is –

ΔV = –m_v x V₁ x Δσ’

Change in the volume per unit time is given as –

∂/∂t (ΔV) = ∂/∂t (–m_v x V₁ x Δσ’)

Assuming that (a) the coefficient of volume compressibility (m_v) remains constant with time and that (b) the change in the volume of soil due to consolidation is negligible, we have –

From Terzaghi’s effective stress principle, we have Δσ = Δσ’ + u. Differentiating both sides with respect to time, we have –

As the total stress, Δσ, is constant with time during the consolidation, that is –

(∂/∂t) Δσ = 0

we have –

Substituting this value in Eq. (11.61), we have –

As the change in the volume of soil is only due to expulsion of pore water –

(∂/∂t) (ΔV) = Δq

Hence, equating Eqs. (11.62) and (11.60), we have –

Here C_vx, C_vy, and C_vz are coefficient of consolidation in x-, y-, and z-directions, respectively. Equations (11.63a) and (11.63b) are the 3D consolidation equations.

Summarizing the assumptions made in the derivation of Terzaghi’s consolidation equation, we have the following:

i. The soil is homogeneous and fully saturated.

ii. Soil particles and pore water are incompressible.

iii. The flow of water during expulsion of pore water occurs only in vertical direction, that is, consolidation is 1D.

iv. The change in the volume of soil due to consolidation is negligible compared to the initial volume of soil.

v. Flow is laminar and Darcy’s law is valid.

vi. Permeability is the same throughout the thickness of the compressible soil layer.

vii. The coefficient of volume compressibility (m_v) remains constant with time.

viii. Compression takes place only due to expulsion of pore water, that is, the effect of secondary consolidation is neglected.

2. Three-Dimensional Consolidation Equation in Polar Coordinates:

For most practical cases, the 3D consolidation is identical about the x- and y-axes. Hence, it is more convenient to express the consolidation equation in polar coordinates consisting of only the radial and vertical axes. The 3D con­solidation in Cartesian coordinates can be transformed into polar coordinates as follows –

x = r cosθ, y = r sinθ, z = z

Hence

r² = x² + y² …(11.64)

and y/x = sinθ/cosθ = tanθ Þ tanθ = y/x …(11.65)

Differentiating Eq. (11.64) partially with respect to x we get –

2r x ∂r = 2x x ∂x Þ ∂r/∂x = x/r = cosθ

Similarly,

∂r/∂y = y/r = sinθ

Differentiating Eq. (11.65) partially with respect to x we get –

∂θ/∂x = y/r² = sinθ/r

Similarly,

∂θ/∂y = x/r² = cosθ/r

The excess hydrostatic pressure (u) is a function of r and θ –

Differentiating Eqs. (11.66) and (11.67) again, adding and simplifying, we have –

For the case of radial symmetry, excess pore pressure (u) is independent of θ. Hence –

∂u²/∂²θ = 0

Therefore, Eq. (11.68) becomes –

Rewriting Eq. (11.63), we get –

For radial symmetry,

C_vx = C_vy = C_vr and x = y = r

Substituting these values in Eq. (11.63), we get –

Substituting Eq. (11.69) in Eq. (11.70), we get –

Solution of 3D Consolidation Equation:

Typical solution for 3D consolidation problem can be obtained by considering the expulsion of pore water in verti­cal and radial directions separately. Thus, Eq. (11.71) consists of two parts as follows –

Vertical flow –

The solution of Eq. (11.72) is given by Terzaghi using Eq. (11.34), which is reproduced below –

where T_z is the time factor for vertical flow and C_vz the coefficient of consolidation for vertical flow.

Radial flow –

The solution of Eq. (11.74) was obtained by Rendulic (1935) using an equation similar to that in the vertical flow –

U_r = f x (T_r) …(11.75)

where U_r is the degree of consolidation in radial direction and T_r the time factor for the radial flow of pore water given by –

T_r = C_vr/(2r) x t …(11.76)

where C_vr is the coefficient of consolidation in radial (horizontal) direction and 2r the effective diameter of a soil cylinder from which pore water flows into the sand drain.

The solution of radial flow problem was obtained for the following two types of vertical strains:

i. Free Vertical Strain Case:

In this case, it is assumed that the consolidation settlements at the surface do not change the distribution of load to the soil. Solutions for this case were obtained by Glover (1930) and Rendulic (1935), assuming that pore water pressure is uniform at a radial distance equal to 2r, which is the effective diameter of the soil cylinder as defined in Eq. (11.76).

ii. Equal Vertical Strain Case:

In this case, the redistribution of surface loads due to arching is considered. As the expulsion of pore water occurs faster near the surface of the sand drains, consolidation (settlement) at any time is more near the surface of sand drain than elsewhere. This would redistribute the stress that is known as arching. In extreme limit, the arching action in soil would redistribute the stresses to such an extent that the consolidation settlement at the surface is the same at all points.

Barron (1948) developed solution for equal vertical strain case, given by the following equations –

U_r = 1 – e^α …(11.77)

where r_w is the radius of sand drains.

It was observed that for values of n > 10, free vertical strain, and equal vertical strain case give more or less same results. As the free vertical strain case requires more time for evaluation, equal vertical strain case is commonly used for solving radial consolidation problems.

Equations (11.73) and (11.77) are combined to form Eq. (11.78) to solve the 3D consolidation prob­lems of sand drains –

(1 – U) = (1 – U_z)(1 – U_r) …(11.78)

where U is the degree of consolidation for 3D flow, U_z the degree of consolidation for vertical flow, and U_r the degree of consolidation for radial flow. HHHH