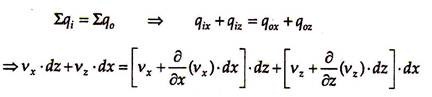Laplace Equation for Two-Dimensional Flow | Soil Engineering

In this article we will discuss about the laplace equation for determining two-dimensional flow of soil elements.

Consider a soil element of infinitesimally small size of dx and dz in X- and Z-directions, respectively, through which the flow is taking place, shown in Fig. 10.8. Consider unit length of the soil element in the Y-direction.

Let v_x be the velocity of flow at the entry in the X-direction and v_z the velocity of flow at entry in the Z-direction. Then the velocity at the exit in the X-direction will be –

v_x + (∂/∂x)(v_x).dx

and the velocity at the exit in the Z-direction will be –

v_z + (∂/∂z)(v_z).dz

Quantity of water entering the element in the X-direction is given by –

q_ix = v_x.(dz.1) = v_x.dz

Quantity of water entering the element in the Z-direction is given by –

q_iz = v_z.(dx.1) = v_z. dx

Similarly, quantity of water leaving the soil element in the X-direction is –

Quantity of water leaving the soil element in the Z-direction is –

Assuming that the flow is steady and incompressible, the quantity of water entering the soil element is equal to the quantity of water leaving the soil element –

Rearranging the terms, we have –

On simplifying, we have –

Dividing throughout with dz x dx, we have –

Let h be the total head at any point. Then the component of hydraulic gradient in the X-direction will be –

i_x = – ∂h/∂x

The negative sign is to indicate that the head decreases in the direction of flow. Similarly, the component of hydraulic gradient in the Z-direction will be –

i_z = ∂h/∂z

By Darcy’s law, we know that –

v_x = k_x .i_x = – k_x . ∂h/∂x

Similarly

v_z = k_z .i_z = – k_z . ∂h/∂x

Substituting these values in Eq. (10.19), we have –

Assuming that the soil mass is homogeneous, permeability will be same throughout in a given direction. Hence –

If the soil is isotropic, then k_x = k_z = k. Then, we have –

This is the Laplace equation for two-dimensional flow.

Summarizing the assumptions made in deriving the Laplace equation, the following may be stated as the assumptions of Laplace equation:

1. The flow is two-dimensional.

2. The flow is steady and laminar.

3. Water and the soil are incompressible.

4. The soil mass is homogeneous and isotropic.

5. The soil is fully saturated and Darcy’s law is valid.

Velocity Potential:

Velocity potential is a scalar function of space and time such that its derivative in any direction gives the component of velocity in that direction. Thus –

ɸ = kh …(10.21)

∂ɸ = ∂x = v_x …(10.22)

∂ɸ = ∂z = v_z …(10.23)

Substituting these in Eq. (10.19), we have –

This is the Laplace equation in terms of velocity potential.

Stream Function:

Stream function is a scalar function of space and time such that its derivative in any direction gives the component of velocity in the perpendicular direction clockwise. Thus a positive stream function when derived would give negative velocity and vice versa, as shown in Fig. 10.9. Referring to Fig. 10.9, we have –

∂Ψ/∂x = – v_z …(10.25)

∂Ψ/∂z = v_x …(10.26)