Design of Check Dam (With Diagram) | Erosion Control | Soil Management

In gully control the structural measures protect the soil against erosion and also help to conserve the rainwater. The earth plugs and check dams form water storage in the gully which can be used as per need, later on. Also, due to obstruction on moving runoff, the soil scouring through gully section gets controlled.

Various design aspects of check dams regarding gully control are outlined as under:

1. Number of Check Dams:

It is determined on the basis of longitudinal profile of the gully. The number of check dams for gully channel can be calculated by using the following formula –

N = [(a – b)/h] … (4.6)

Where,

a = total vertical distance. It is calculated based on the average gully bed gradient and the horizontal distance between the first and last check dams in that portion of the gully bed.

B = total vertical distance. It can be computed on the basis of compensation gradient and horizontal distance between the first and last check dams in that portion of the gully bed.

H = average effective height of check dam, excluding the depth of foundation.

2. Spacing of Check Dam:

The spacing between check dams is determined on the basis of compensation gradient and effective height of the check dams. The compensation gradient refers to the gradient between the top of lower check dam and bottom of the upper one. Figure 4.7 shows the view of measurement of com­pensation gradient and gully bed gradient. The compensation gradient is the future or final gradient of the gully channel.

It is formed when materials carried by flowing water fill the check dams to spillway level. Experimentally, it has been observed that the compensation gradient of gullies is not more than 3%. The location of first check dam should be at a stable point of the gully. The points such as rock outcrop, the junction point of the gully to a road, the main stream or river etc., are normally preferred for locating the first check dam.

In the condition, when such stable points do not exist, then a counter-dam should be constructed. The distance between the first dam and the counter-dam should be at least two times the effective height of first check dam. At the second point, the effective height of second check dam is marked at the edge of the gully by considering gully depth, depth of spillway and maximum height of the check dam.

While deciding the construction of check dams, the narrowest parts of gully should preferably be taken into account, because at such points the construction cost of check dam gets reduce. In this case, to establish the compensation gradient between the proposed check dams, the foundation depth of upper check dam should be proportionately increased to extend the spacing between the lower and upper check dams.

And spacing can be shortened by decreasing the foundation depth. As precautionary measure the depth of foundation should not be increased to the extent that the total height of check dam (effective height plus foundation depth) becomes more than the maximum permissible total height.

3. Maximum Discharge and Spillway Dimension:

The maximum discharge (Q_max) of the gully catchment to be handled by check dam can be computed by using the Rational formula, given as under –

Q_max = CI A/3.6 … (4.7)

in which, C is the runoff coefficient, varies from 0.20 to 0.50 depending on the soil type, land use and topography; I is the rainfall intensity, is determined based on the time of concentration of the flowing water from the bounding of catchment to the point of check dam location. The rainfall intensity should be calculated based on the maximum (one hour) rainfall intensity (mm/h) with 5 to 10 years return period; and A is the area of gully catchment above the proposed check dam (sq km). The value of Q_max is obtained in the unit of m³/s. The Rational formula is suitable to use only when rainfall intensity (I, mm/h) data of given frequency is available.

However, if there is no intensity data, then using the following formulae the discharge rate can be predicted:

In which, A is the area of catchment of gully above proposed check dam (sqkm); Q_mm is the maximum discharge of the gully catchment at the proposed check dam (m³/s) and a is the coefficient varies from 0.6-2.0 depending on the type of land use. If there already has been developed such relationships for the proposed area, then they must be used for computing the runoff. As precautionary measure, before using any empirical formula they must be verified for the given area. If it is found suitable then it should be used, otherwise no.

General Run-off Formula –

Q = AV … (4.10)

in which, A is the cross-sectional area (wetted area) of main gully for the highest flood water level at the proposed check dam site (sqm); and V is the velocity of flowing water at that point (m/s). The value of V can be computed by using the Manning’s formula, given as under –

In which, n is the Manning’s roughness coefficient of gully. For gully section the value of n can be taken as 0.025; R is the mean hydraulic radius, which is the ratio of wetted area to the wetted perimeter (m) of gully section. The value of R is computed for the point where cross-sectional area of the gully has been measured considering highest flood level; S is the gully gradient (%) and V is the velocity of flowing water at the proposed check dam site (m/s).

The simple Kresnik formula estimates more accurate value of Q_max for the gullies having the catchment area less than 20 ha. However, in case of torrent an accurate value of Q_max can also be computed by using this formula for the catchment of maximum 300 ha area.

4. Spillway Dimension:

The dimension of spillway used in check dam for safe disposal of runoff, can be computed by using the following formula –

Q = CLD^3/2

in which, C is the coefficient taken as 3.0 for loose rock, boulder log and brushwood check darns, and 1.8 for gabion and cement masonry check dams; L is the length of spillway (m); D is the depth of spillway (m) and Q is the maximum discharge of gully catchment at the proposed site of check dam (m³/s).

Stability of Check Dams:

Gravity or Bulk Dams:

The check dams constructed by using loose stones, boulders, gabions and cement-masonry materials are called “gravity dams” or “bulk dams”. The slope of downstream face is kept backward and of upstream face it is generally vertical. The stability of check dam is evaluated against overturning, collapsing or sliding actions. The dam weight and water flowing through its spillway section act vertically downward; and the pressure on its upstream face due to filled materials to the spillway level acts in horizontal direction.

The resultant of vertical and horizontal forces passes through the foundation, at the distance of at least two-third of its width. For stability points of view the weight of check dam should not exceed 50 tons/m² or 5 kg/cm². If the pressure on the ground is less than 5 kg/cm², and pressure curve crosses the foundation base at five-sixths of its width, then check dam is considered to be under safe condition.

Loose Rock and Boulder Check Dams:

These are relatively small check dams. Their height is maximum up to 2 m including foundation depth. The pressure on the ground is always less than 5 kg/cm². In these check dams the water pressure or pressure due to mixture of water, soil, sand, pebbles etc. acts on the filled materials; not directly on the dam’s upstream face. The design of loose rock check dams is not done by considering the hydrostatic pressure.

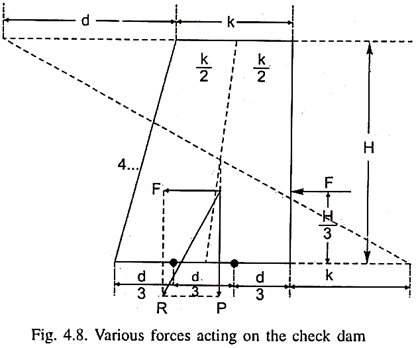
If there is mudflow in the gully, then consideration of hydrostatic pressure should be there, because mudflow contains few percentage of water, which develops hydrostatic pressure. The line of action of hydrostatic pressure varies from 1.8 to 10 times of water depth. Various forces acting on the check dam are shown in Fig. 4.8.

Construction Procedure:

The following points are taken into consideration for construction of check dam to control the gully:

i. The construction of check dams or earth plugs should be started from the lower end of gully; and proceed to the upward.

ii. If rock materials are required to transport from the lower end to upper end of gully for check dam construction, then construction should be started from the upper end of gully.

iii. Before starting the construction of check dam the gully head should be stabilized by constructing suitable check.

iv. The activities must be planned in such a way that all construction works would get complete before rainy season. Otherwise, there is possibility of damage of incomplete structure.

Maintenance of Check Dam:

It is done under following aspects:

i. The maintenance of check dam must be continued for at least two years after treatment year.

ii. The treated areas should be kept in proper inspection for at least one year.

iii. The trees and grasses established in gully catchment should be protected against fire, illegal wood-cutting, grazing and encroachment. If the re-vegetated areas are properly managed for several years after treatment, then some fuel wood gets produced from tree plantations; and fodder can also be obtained from the grasses and tree plantations.

Spacing of Temporary Structures:

The small dams, usually 0.4 to 2.0 m in height, which are made of locally available materials like, earth, wooden planks, poles, brush wood or loose rock across the gullies to dissipate the erosive nature of flow velocity and finally to trap the sediments, which is helpful in reducing the gully depth and slope, both. Although, these structures are temporary, but provide a good measure for gully control. In order to make these structures more stable, the agronomic treatments are also used in combination.

The agronomic treatment includes the planting of trees, shrubs and grasses in surrounding lands. These treatments reduce the overload on temporary structures, as result the life span of these structures gets increased. Apart from above, they must be designed properly; should have provision to spill the water very smoothly and their location as well as spacing should also be in proper way. Heed (1976) developed following formula to determine the spacing of check dams –

Spacing = HE/k tan θ . Cos θ … (4.12)

Where,

HE = dam height, measured from the crest of spillway to the gully floor.

k = constant, its values are given as:

* For tan θ < 0.2, k = 3.0

* For tan θ > 0.2, k = 0.5

Heed also recommended following points for use of temporary gully control structures:

1. The loose rock dams are economical for the heights up to 0.45 m; the single fenced brush wood dams are economical for the heights ranging from 0.45 to 0.75 m and double row brush wood dams are for the heights of 0.75 to 1.0 m. The depth of gully for these dam heights is 1.2 m, 1.2 to 1.5 m and 1.5 to 2.1 m, respectively is most suitable.

2. These dams should be keyed into the gully banks to make them more stable against sliding.

3. At downstream side an apron should be constructed on gully bed to check the flow against undercutting of the structure.

The length of apron for different slopes of gully bed is given as under:

(i) For gully bed slope of 8.5° the length of apron should be 1.5 times the height of structure.

(ii) For steeper slope than 8.5° the apron length should be 1.75 times the height of structure.

4. Towards down-stream side of the apron, loose rock sill of about 0.15 m in height should also be constructed for creating the pool and dissipating the energy of falling water from the crest of spillway.

5. The spillway should be designed to handle the peak runoff rate of a given return period, usually 25 years. The cross-section of spillway should be preferred trapezoidal with bottom breadth less than the width of gully. Greater width of spillway is not desirable, because flowing of water over spillway is likely to strike on the either sides of the gully, where erosion protection measures are absent. After fixing the breadth of spillway the depth is determined using the weir formula.

The following formula can be used for computing the depth of spillway:

Where,

D = depth of spillway (m)

Q = peak discharge of the gully (m³/s)

L = bottom width of spillway (m).

And for a spillway with the side slope 1 : 1, the top breadth (L_t) of spillway can be obtained as –

L_t = L + D … (4.14)